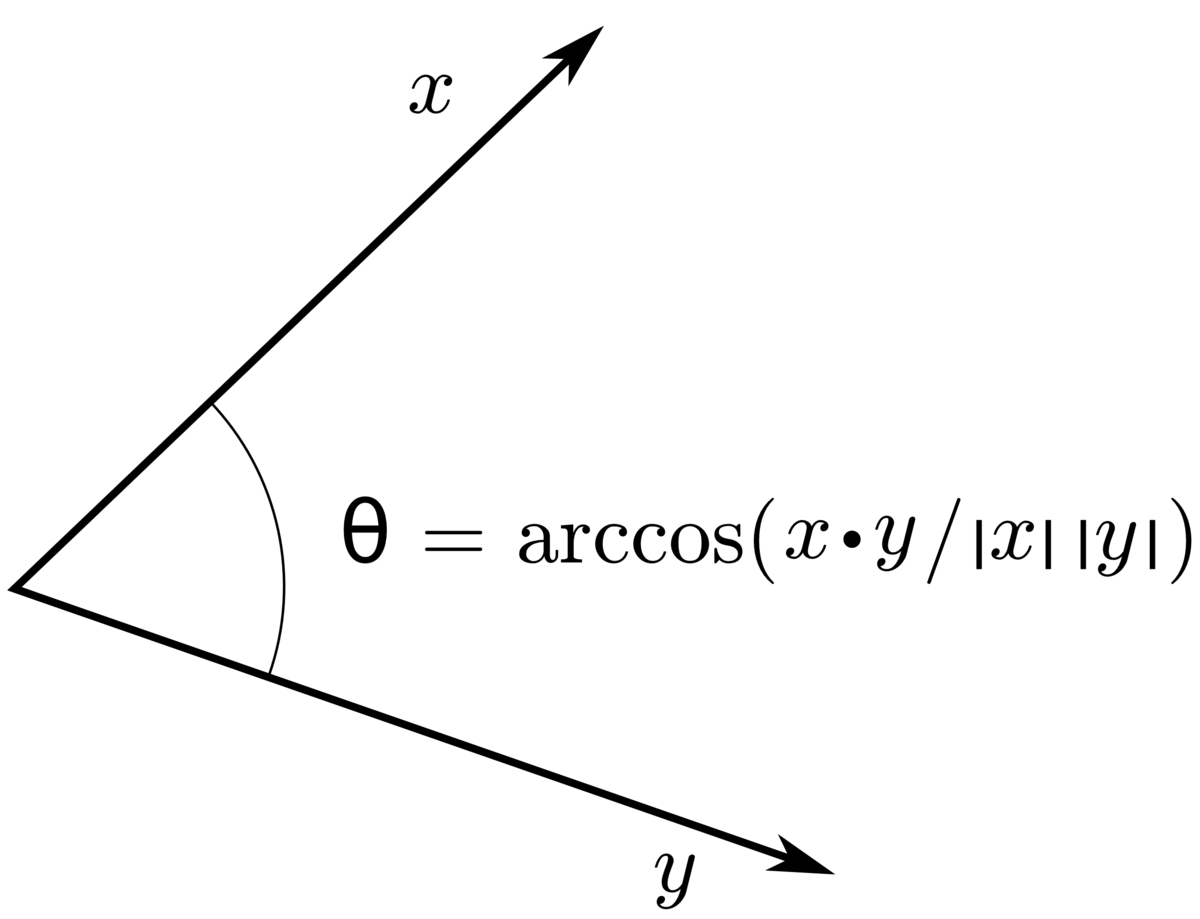
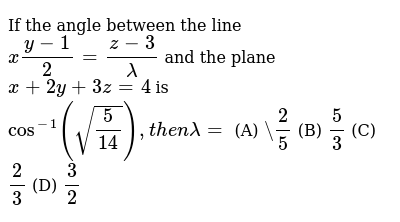Angle Between 3d Vector And Plane

How to calculate the angle between a plane and a vector all 3d coordinates.

Angle between 3d vector and plane. Contrarily the angle between a plane in vector form given by r a λ b and a line given in vector form. The plane contatining both vectors is an arbitrary and is not parallel to xy or any other of cardinal planes vn is a plane normal both vectors along with. Now the angle between the line and the plane is given by. Where x 2 y 2 z 2 represents the coordinates of any point on the plane.

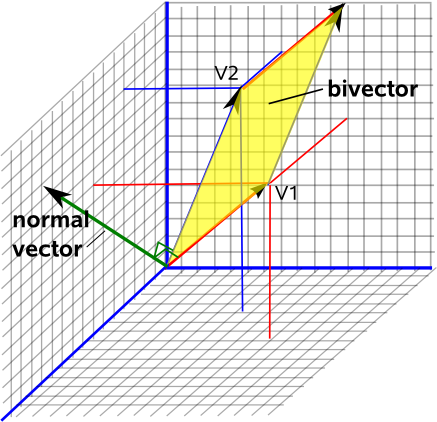
Calculate a normal n to the plane as the cross product of plane1 plane2 and plane1 plane3. Honestly between the direction vector v 10 5 5 and the normal vector 2 1 4 the angle is not acute in fact it is obtuse you can see that by a simple plot. Introduction to planes when introduced to the 3d coordinate system we are introduced to the concept of math planes and vector equations for planes. If you rotate it in a plane that does not include u then the angles differ.

Find the angle between them. The vector op has initial point at the origin o 0 0 0 and terminal point at p 2 3 5. The angle between two vectors in 3d. Examples of tasks with angle between line and plane example 1.

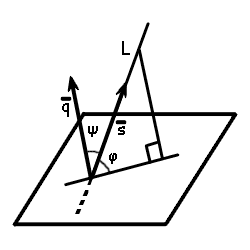
The angle between a line and a plane is equal to the complementary acute angle that forms between the direction vector of the line and the normal vector of the plane. Eigenvectors are the vectors for which the angle between and is 0. Math planes are used frequently with vectors when calculating normal vectors to planes or when finding the angle between two planes. Possible issues 1 the angle between the zero vector and any.

A 2 2 b 2 2 c 2 2 vector form. The equation of the plane in the vector form can be given by. Sin ɵ a 1 a 2 b 1 b 2 c 1 c 2 a 1 2 b 1 2 c 1 2. The angle between a line r and a plane π is the angle between rand its orthogonal projection onto π r.

It is simpler to find the equations of math planes that is formed by two axes or a plane that is parallel to one. We saw earlier how to represent 2 dimensional vectors on the x y plane. What i need is a signed angle of rotation between two vectors va and vb lying within the same 3d plane and having the same origin knowing that. Using the formula of the scalar product of vectors and module of vectors in coordinate form we obtain the formula for calculating the angle between the line and the plane.

So we have vec b 6i 2j 3k and vec n 3i 4j 12k. The vector angle is related to the cross product through. Arctan of two arguments gives the signed vector angle between the axis and the vector. Now we extend the idea to represent 3 dimensional vectors using the x y z axes.

See the 3 dimensional co ordinate system for background on this. The equation of a plane is 3x 4y 12z 7. Since φ 90 ψ then the sine of the angle between the line and the plane is sin φ cos ψ. However as you are asking about the angle between a line and a plane so the you must take care of the orientation of the vectors you are working with.

We can draw the vector op as follows. Let θ be the angle between the line and the normal to the plane.